数字图像处理笔记-第五章：图像恢复

5. 图像恢复

5.1 退化模型

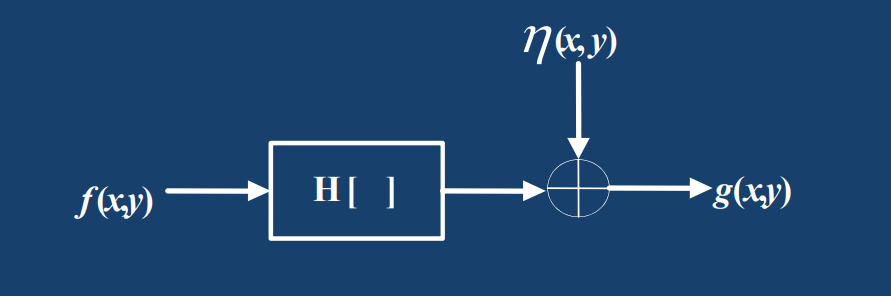
图像恢复处理的关键在于建立退化模型。建立退化模型是指根据已有的先验知识，对模糊或噪声等退化过程进行数学模型的建立核描述。

其中矩阵为退化模型，也可以用表示，为噪声。

时域上，退化模型加上噪声可表示为

频域上则可表示为

进行FFT之前应先将和进行周期延拓

退化矩阵是一个循环矩阵（类似于自相关矩阵），循环矩阵式一定可以被对角化的，也就是说，存在对角阵和特征向量矩阵，使得

那么一幅图像的退化模型则可表示为

若采用的是FFT，则就是FFT的变换矩阵(构成的矩阵)，且对角阵就是。

5.2 无约束复原-逆滤波法

5.2.1 逆滤波的步骤

图像的无约束复原主要指逆滤波（也称反向滤波）法，逆滤波法没有考虑噪声影响。

据说图像算法相关的岗位面试也经常问逆滤波的有关问题

不考虑噪声的情况下，5.1节的退化模型就变为

如果对右侧等式两边同时乘以，就成了FFT后的形式

写为频域表达式为

即为反向滤波器。

由于这个式子把乘到作编去就是正向退化滤波的形式，所以复原的过程称为逆滤波

5.2.2 逆滤波法的特点

5.2.1中的逆滤波没有考虑噪声，如果将噪声项加入逆滤波，最终恢复的图像具有如下形式

显然可以看出，右边等式当的值比较小的时候，噪声项的影响会很大，使得图像淹没在噪声中。

因此，使用逆滤波有三点注意事项

1. 在处不做计算（防止除数为0）

2. 当很小时，噪声项起主导作用，而实际上离开原点后衰减的很快，所以复原应当局限于离原点不太远的有限区域进行，可以理解为将过一个理想低通滤波器

3. 为了避免振铃效应，可以对逆滤波进行加门限的处理