随机信号处理笔记-第二章：维纳滤波

维纳滤波的本质是最小化期望信号与系统输出信号之间的均方误差，是一种线性滤波器，可以与最小二乘线性预测那一套方法相关联。

1. 滤波、预测和插值

通过目标信号与当前信号的时间关系确定属于滤波、预测或者插值

已知，期望输出

2. 维纳滤波的时域解

2.1 最小均方误差

最小均方误差(Minimum Squared Error)定义为期望信号与输出信号差值的平方

要求MSE最小，可以用上式对求偏导，对每一个取值，有

令上式等于0，即可得到最优，也就是2.2中的维纳霍夫方程，这里不再做推导。

2.2 时域维纳滤波

2.2.1 维纳霍夫方程

维纳霍夫方程(Wiener-Hopf Equation)表示的是输入的自相关和输入输出之间的互相关之间的联系

其中为最佳维纳滤波器。用矩阵表示，即可得到维纳霍夫方程

其中为输入的自相关，为输入与输出的互相关，为滤波器，即。

2.2.2 非因果IIR维纳滤波

求解时很容易想到将等式两边同时做变换，可得到

注意：变换存在的条件是该信号是双边序列。也就是说，用这个式子表示的在时域上的，即不存在约束条件。实际上，直接通过变换得到的称为逆滤波，逆滤波是维纳滤波的一种特殊情况（详见数字图像处理笔记第四章维纳滤波部分）。但无论是否有约束，时域上的维纳霍夫方程始终成立。

因果IIR维纳滤波将在第3节与白化滤波器一起介绍

2.2.3 FIR维纳滤波

回顾代价函数MSE，若把有限长输入信号与滤波器都写为向量的形式

则2.2.1中的代价函数可写为

因为和都是标量，，所以有。

因此，关于滤波器的代价函数用矩阵可以表示为

注意：式中所有项都是标量，因此也是一个标量

对求偏导可得

令上式等于0，可得出FIR维纳滤波的时域解

上述方式是通过求导来得到维纳滤波器的最优解。实际上，观察的表达式，它是关于的一个二次函数，可以通过矩阵配方的形式将其转化为顶点式，由于矩阵配方的过程非常复杂，这里直接给出结果

可以直观看出当时，符号为正的第三项等于0，此时有最小均方误差

2.2.4 正交性原理

2.2.1中，为了求得最佳滤波器，令误差对滤波器的偏导数等于0，等价于下式

这是正交性原理的第一个核心表达式。从该式可以得知，MSE最小时与正交。

令输出信号为，根据离散时间滤波器的定义，是的线性组合，因此也应当与误差正交

这是正交性原理的第二个核心公式。

正交性原理可以总结为：

• 误差与观测数据正交
• 误差与估计信号正交

正交性原理与MSE之间互为充要条件，即33

从图中也可以直观理解，只有当误差同时垂直于和时最小。

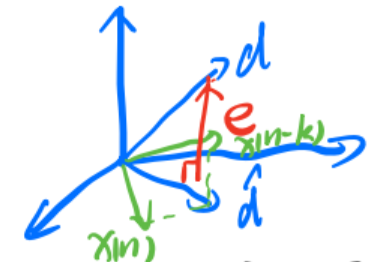
3. 维纳滤波的频域解

3.1 因果IIR维纳滤波

本节主要考虑输入信号为白噪声时的情况。

白噪声的特点是自相关矩阵的对角线元素，其逆矩阵的对角线元素为

将白噪声的自相关矩阵带入维纳滤波的时域解有最佳滤波器（用表示）。

为单位阶跃函数。

对其进行变换有

就是因果IIR维纳滤波的频域解形式，一般情况下因果IIR维纳滤波的求解比较困难。

将带入最小均方误差中有

3.2 白化滤波

3.1中假设了输入为白噪声，若不是白噪声，则可以先将白化为白噪声，再进行维纳滤波操作。若的功率谱时有理分式，则可以看作是一个滤波器对白噪声的响应。如图所示

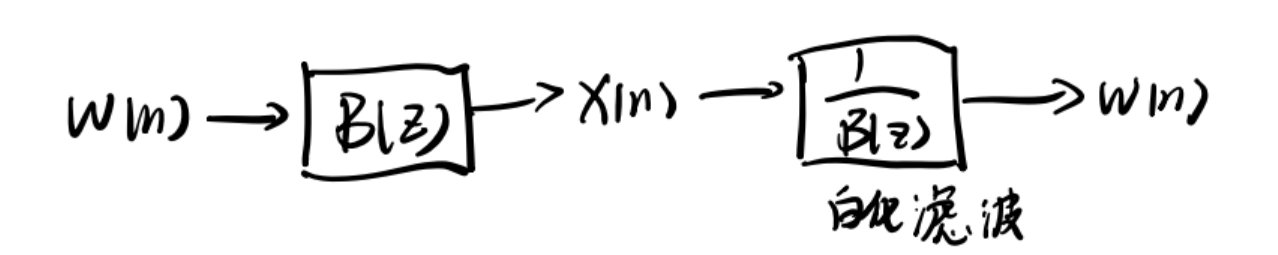
这里才是白化滤波器，表示白噪声经由一个滤波器变为信号的过程。

根据相关卷积定理和自相关与卷积的关系可得

证明：

根据相关卷积定理： 根据卷积与自相关的关系： 则 两边同时做变换有

是一个最小相位滤波器，也就是说它的零极点都在单位圆内。根据第一章4.1.3的结论，还可以知道存在一对实部与互为倒数的共轭极点。

现在，我们可以采用相同的方式用白噪声得到期望信号，假设白噪声通过一个系统得到期望信号，如图所示

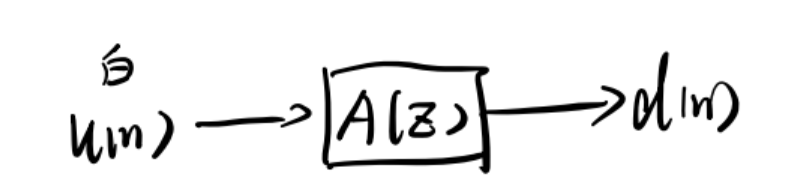
那么就可以得到基于白化滤波器的维纳滤波器，整个系统如图所示(画的有点潦草但应该还看的清orz)

这个系统的意思是，假设用将白噪声转换为期望信号，而被其它噪声污染得到了我们现实生活中实际到手的信号，通过一个白化滤波器，得到白噪声，这样就可以使用2.3.1中得到的维纳滤波器来还原信号，和联合起来形成了我们拿到的输入需要经过的系统，而通过得到的信号是估计信号，我们希望通过去还原出原始信号使得与的MSE最小。

显然有

可以证明，将其带入有

例：证明

证： 命题等价于证明： 根据互相关函数的性质有： 又有 带入有

将替换为有

两边同时做变换，命题得证 （上课时老师说这道题也可以用相关卷积定理证明，但我这里没有证出来，如果有会用相关卷积定理证明的同学非常欢迎联系我！！）

3.3 非因果维纳滤波器的简单分析

2.2.2节介绍了非因果IIR形式的维纳滤波，这里主要从画图的角度分析一下非因果滤波器的形式。

首先需要知道非因果滤波器的一般形式，假设，为噪声，这里对应白化滤波器图中间的位置。

因为噪声与期望信号是无关（）的，因此容易证明

同理可得

第二个公式可以简记为和的自相关=自相关的和。

根据相关卷积定理，可得

用替换就可以得到滤波器的功率谱形式

例：

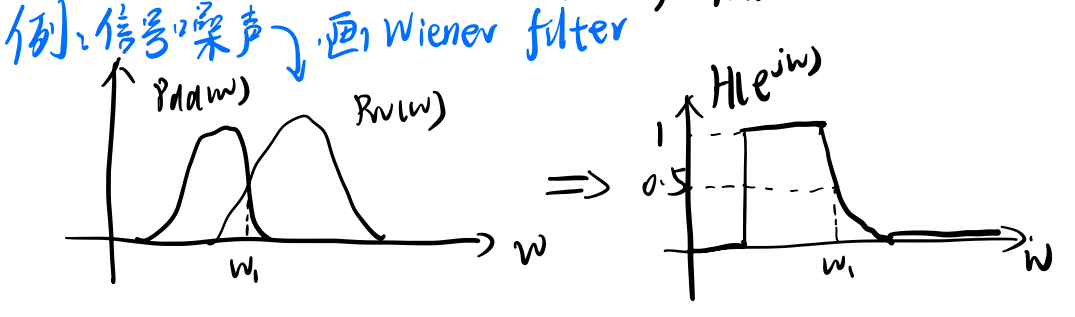
简而言之，就是有信号就开，没信号就关，没噪声就全通，有噪声就降幅度

3.4 一道例题

设计白化滤波器，使其具有功率谱为的信号白化

思路：凑形式，待定系数求

解：

回顾与白化滤波器的关系

是在处的特殊形式，因此需要将凑出的形式。根据欧拉公式

替换为

我们知道白化滤波器的倒数一定具有的分式形式，因此可以根据待定系数法求和。

直接令，有

因此

最后记得倒一下

4. 维纳滤波器小结

含义	公式
最佳因果FIR维纳滤波	，
最佳非因果IIR维纳滤波
最佳因果IIR维纳滤波
均方误差表达式
最小均方误差
正交性原理

5. 维纳预测器

概念：已知，求信号未来的估计值。

一般的，为噪声，若，即没有噪声时称为纯预测。

5.1 N步因果纯预测器

令预测器期望输出为，则此时与的互相关存在如下关系

做变换则有

将其带入3.2节中带白化滤波的因果IIR滤波器

由于，可以得到下列一长串等式

将的关系带入，就得到了N步因果纯预测器的公式

注意这里不能消掉，因为中括号里的只代表右边序列的变换。

解题的过程中，要灵活运用的关系。

N步纯预测器的最小均方误差为

这里就不做详细推导了。

5.2 一步线性预测

转换一下N步线性预测的概念，令，已知，预测

预测值是前面个已知值的线性组合

为了后续表示方便，我们改变一下滤波器系数的表示方式，令

为了使MSE最小，同样采取对系数求偏导的方法，经过一系列运算最终可以得到如下矩阵方程

该方程称为Yule-Walker方程，其中。这个矩阵方程就是是求解一步预测器的方法，求解阶一步线性预测器时直接列出对应方程即可求解。

6. 新息

定义：实际观测值与预测值的差值定义为新息，用数学表达实际上就是不带绝对值的L1距离。

若从起点开始预测，新息有以下三条性质：

性质1：，即新息与之前的观测值都没有关系，这条性质实际上就是正交性原理

性质2：

性质3：，即观测值与新息存在一一对应的关系，知道观测值就可以求新息，反之亦然