数字图像处理笔记-第三章：图像变换

发表于 更新于 分类于 阅读次数： 本文字数： 13k 阅读时长 ≈ 11 分钟
数字图像处理笔记-第三章：图像变换

3. 图像变换

3.1 图像变换的基本概念

线性空间中，如果是一个向量，是一个矩阵，则称

是向量到向量的线性变换。

若阶矩阵满足

则称位正交矩阵，称为正交变换。

3.2 图像的几何变换

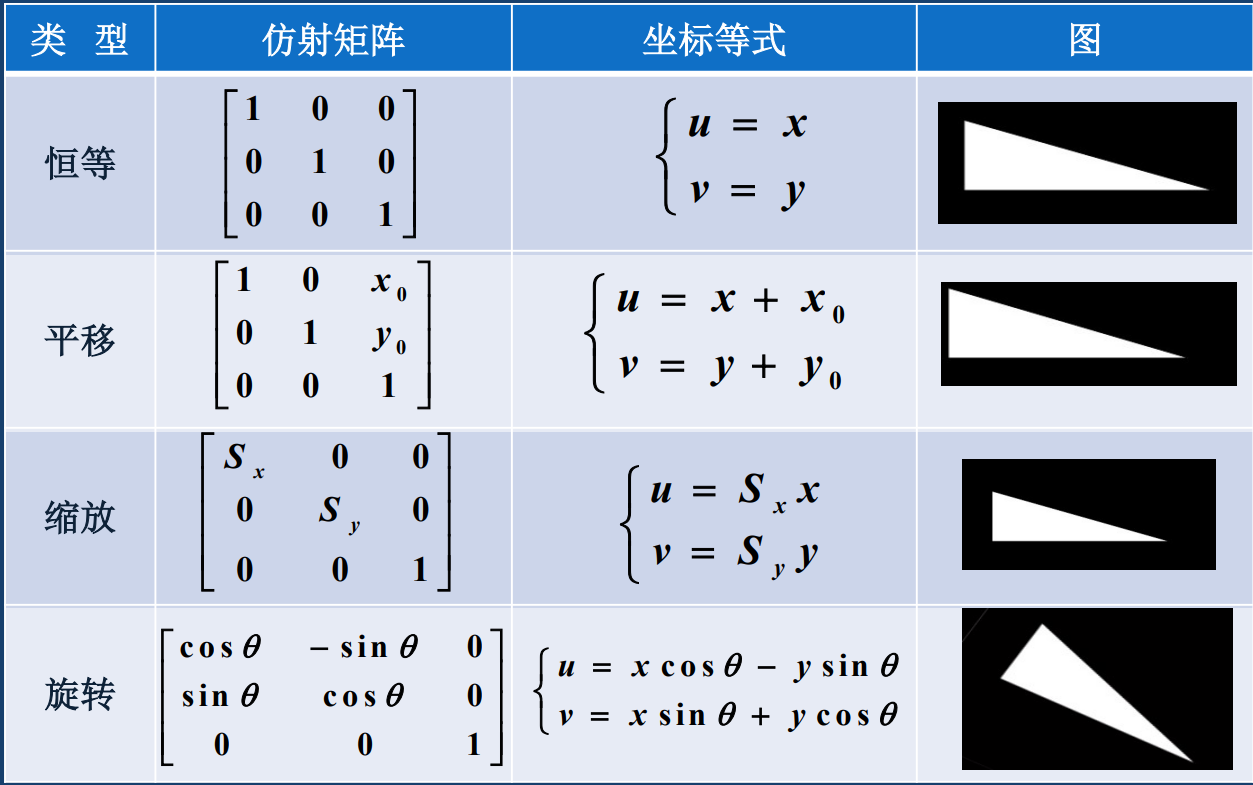
几何变换是最通用的变换之一，例如平移、旋转、裁剪等，这些效果展示目前基本都已经集成到了手机的相片编辑系统中。

3.2.1 平移变换

假设平移前坐标为，后新坐标为，坐标平移量为，则平移变换可以用矩阵表达为

3.2.2 比例缩放

设为缩放系数，则比例缩放可用矩阵表达为

3.2.3 旋转变换

将输入图像绕笛卡尔坐标系原点旋转角度，用矩阵表示为

思考：旋转变换矩阵的n次方是什么？ 从旋转的物理意义出发，每乘以一个旋转矩阵，就相当于将原图像旋转了角度，那么乘以n个旋转矩阵，则相当于旋转角度，那么旋转矩阵的n次方就可以写为

需要注意的是，对于图像的旋转操作会由于图像空间量化误差而造成信息上的损失，如下图所示

旋转引起的量化误差信息损失

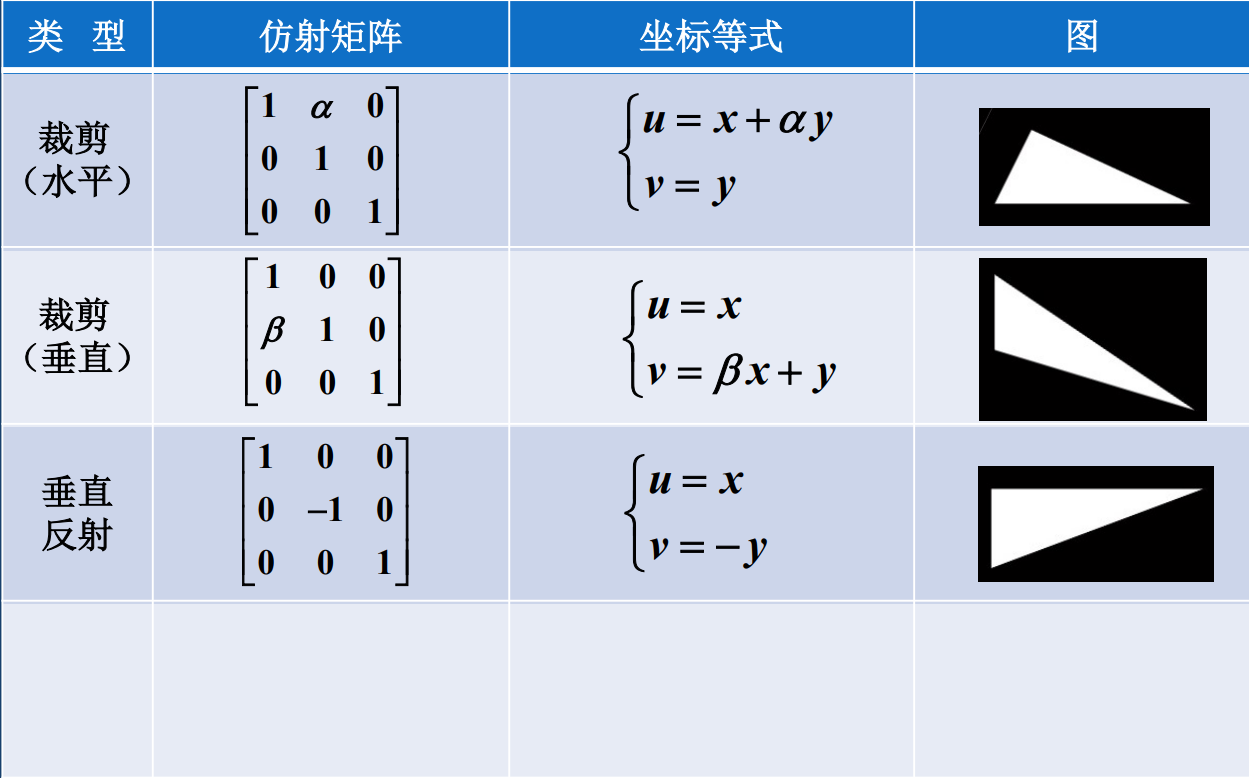
3.2.4 仿射变换

仿射变换是前面几种变换一般形式，仿射变换具有：

  • 平直性，即变换前后都是直线
  • 平行性，即变换前后平行的线仍然平行

仿射变换的一般表达式为

通常，仿射变换都会将变换矩阵与坐标增广一个维度，如下所示：

这样做的好处是将仿射变换矩阵变为了方阵，可以进行矩阵的连乘，即多个仿射变换连续进行。

仿射变换的性质：

  1. 仿射变换只有6个自由度，对应矩阵前两行的6个元素，因此仿射变换可以保证变换前后平行的直线仍然是平行，三角形仍然是三角形，但不能保证四边形以上的多边形映射仍为多边形
  2. 仿射变换的乘积和逆变换都是仿射变换
仿射变换总结
仿射变换总结2

3.2.5 透视变换

与仿射变换不同，透视投影按照桶投影中心这一点出发的直线将物体投影到图像平面。透视变换矩阵表达式为

透视变换有9个自由度，因此可以实现平面四边形到四边形的映射。

3.3 图像插值

3.3.1 最邻近插值

最邻近插值也叫零阶插值，也就是令变换后像素的灰度值等于它最近的输入像素的灰度值。最邻近插值输入输出关系为简单的比例关系，

这里直接给出最邻近插值的Python代码

1
2
3
4
5
6
7
8
9
10

def nearest(img, scale):
    w, h, _ = img.shape
    n_width = w*scale
    n_height = h*scale
    n_img = np.zeros((n_width, n_height, 3))
    for c in range(3):
        for i in range(n_width):
            for j in range(n_height):
                n_img[i, j, k] = img[round((i-1)/scale), round((j-1)/scale), c]

最邻近插值计算简单，但若scale比较大时会出现锯齿边缘的效应，插值效果较差。

3.3.2 双线性插值

双线性插值也叫做一阶插值，该方法简而言之就是先沿图像矩阵的行插值，得到结果后再对图像列插值，因此需要至少4个点（行2个，列2个）来进行双线性插值，一张图可以说明这个方法1，先通过横向插值得到中间处上方的第一个值，同理用得到出下方的值，然后这两个值再做一次插值即可得出最终结果

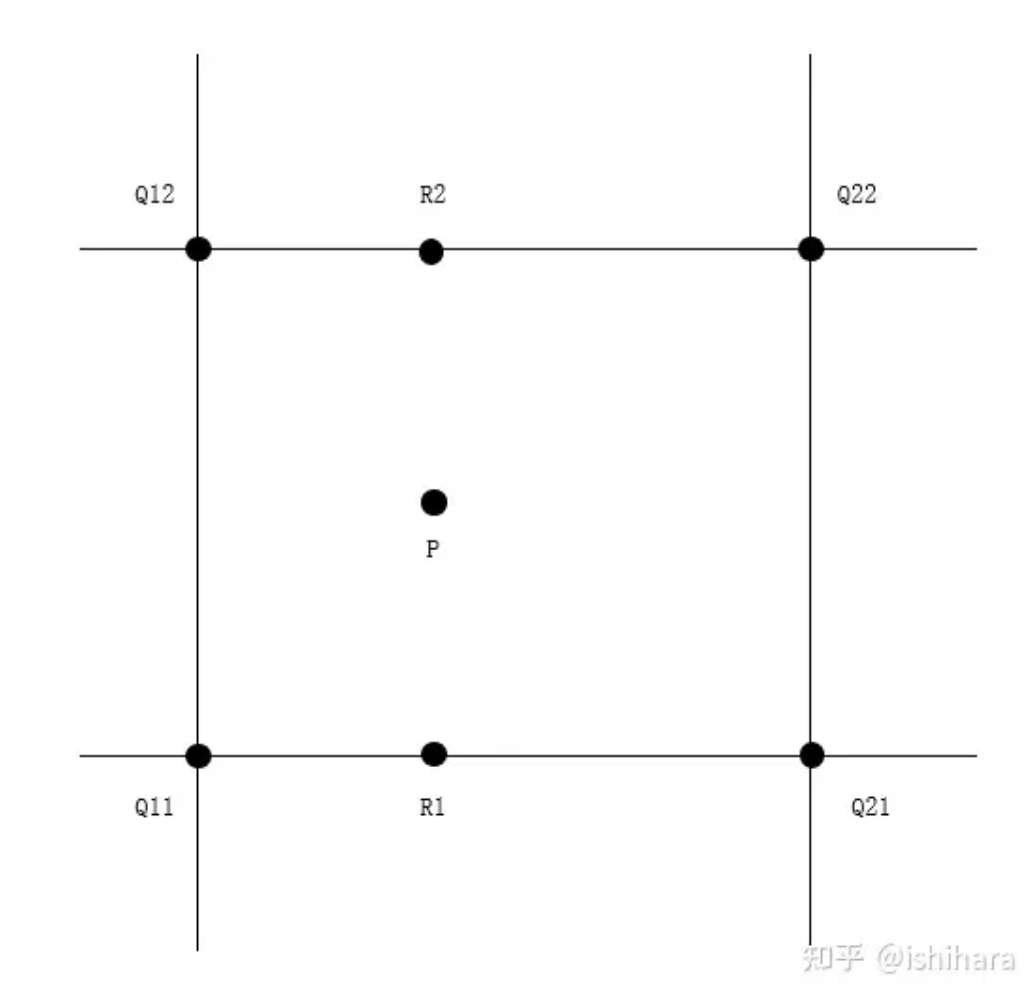
双线性插值

具体公式如下，总体原理是根据到和到之间的斜率相等列出等式，然后做数学变形计算出处的值，其余同理。

将，带入有：

同样给出Python代码，实际操作中双线性插值只用相邻4个点（像素位置差1），所以这里分母全为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def double_linear(img, scale):
    width, height, channel = img.shape
    n_width = int(width*scale)
    n_height = int(height*scale)
    for c in range(channel):
        for i in range(n_width):
            for j in range(n_height):
                src_x = i / scale
                src_y = j / scale
                src_x_0 = int(np.floor(src_x))
                src_y_0 = int(np.floor(src_y))
                src_x_1 = min(src_x_0 + 1, width - 1) #确保不会选到图像外的点
                src_y_1 = min(src_y_0 + 1, height - 1)
                value0 = (src_x_1 - src_x)*img[src_x_0, src_y_0, c] + (src_x - src_x_0)*img[src_x_1, src_y_0, c]
                value1 = (src_x_1 - src_x)*img[src_x_0, src_y_1, c] + (src_x - src_x_0)*img[src_x_1, src_y_1, c]

                n_img[i, j, c] = int((src_y_1 - src_y))*value0 + (src_y-src_y_0)*value1

                return np.array(n_img)

双线性插值的缺点是边界有模糊，因为这样插值相当于对选取的四个点做了加权平均。

3.3.3 卷积插值法

图像放大时，图像像素的灰度值插值可以通过卷积实现，即将输入图像两行两列中间插入0，然后通过低通模板滤波。

3.4 图像的傅里叶变换

3.4.1 回顾1D-DFT

对于有限长序列，，其DFT定义为

将上述表达式转化为矩阵表达式：

其中，为变换矩阵，且是对称的，即

此外，还可以证明为酉矩阵(unitary matrix)， 即

因此有

而1D-DFT则为正交变换，正交变换的反变换可用该矩阵表示

3.4.2 2D-DFT

2D-DFT是对1D-DFT的扩展，公式如下

3.4.3 2D-DFT的性质

重点

可分离性、移位性、频谱中心化、尺度变换和平均值考试请务必牢记

性质 描述 数学表达式
变换核可分离性 2D-DFT相当于先对行（或列）做一维DFT，再对列（或者行）一维DFT
移位性 分为空间移位、频域移位，移位前后幅度不变 空间移位： 时间移位：
频谱中心化 对于大小的图像，将图像的频谱从远点搬移到中心
旋转不变性 空域中旋转角度，频域中也旋转同样的角度
卷积定理 空域卷积<=>频域相乘，频域卷积<=>空域相乘，需要注意的是需要先将扩展至大小，防止卷积时与前一个周期重合
周期性 2D-DFT变换前后是周期的
共轭对称性 若图像为实函数，则具有共轭对称性
线性 傅里叶正反变换都是线性变换
尺度变换 空域相乘，频域相除还要除以放缩尺度的乘积
实偶函数DFT 仅有余弦实部，奇部求和为0
实奇函数DFT 仅有正弦虚部，偶部求和为0
平均值 对整幅图像求平均，相当于，需要注意空域与频域两种求法
相关定理 空域互相关<=>频域滤波器变为共轭相乘，反之亦然

3.5 图像变换的一般表示形式

3.5.1 图像变换一般表达式

图像的变换多种多样，仿射变换和傅里叶变换只是其中的两个例子，我们可以用一般形式表达图像变换：

其中为正变换核，称为反变换核。在傅里叶变换中，。

3.5.2 正交变换

上述表达式的正变换可以用矩阵形式记为

其中为变换矩阵。

  • 若实数方阵满足，则为正交矩阵
  • 若复数方阵满足，则为酉矩阵

正交矩阵（酉矩阵）性质如下

性质 描述
逆与转置 或者
正交归一 正交矩阵始终有：行模=列模=1，且不同行列向量之间正交
行列式 正交矩阵行列式
反身性 若为正交或酉矩阵，则和也为正交或酉矩阵
矩阵连乘 若为正交或酉矩阵，则也为正交或酉矩阵

变换矩阵为正交（或酉）矩阵的变换称为正交变换，如2D-DFT即为正交变换 二维正交变换同样遵循帕西瓦尔定理(Parseval law)，即空域上图像的平方和等于频域上频谱的平方和

3.5.3 可分离变换

若变换（或反变换），则称该变换为可分离的，注意不是和，牢记： 。

如果一个变换核是可分离的，那么一个二维可分离变换可由两个一维变换完成，例如2D-DFT。如果将变换矩阵分离为两个变换矩阵，则可分别乘在原始信号的左右分别表示行变换和列变换

如果存在逆矩阵，则可写出反变换

因为为正交矩阵，有，因此上式又可以写为

由于DFT是复数运算，运算量大，不便于实时处理，所以通过构造函数使其变为偶函数，偶函数的2D-DFT仅含余弦实部，形成的变换又称为离散余弦变换(Discrete Cosine Transform, DCT)。

3.6 离散沃尔什-哈达玛变换

重点

沃尔什-哈达玛变换(Walsh-Hadamard Transform)的变换矩阵由+1和-1组成，对应两个数值逻辑状态，计算机更容易实现。图像数据越是均匀分布，经过沃尔什-哈达玛变换后的数据越集中在矩阵边角，因此沃尔什变换可以集中图像能量，把一个矩阵的非零元素压缩到边角上，可以用于压缩图像信息编码。

3.6.1 哈达玛变换

哈达玛矩阵可分为多阶递推矩阵，其中最低阶矩阵为

递推矩阵为

最低阶矩阵及其递推矩阵需记忆

如二阶哈达玛矩阵

注意矩阵每一行变号次数分别为0,3,1,2，是乱序的。

哈达玛变换核有3条性质：

性质 描述
递推性 可由递推得到
正交性 哈达玛变换矩阵为实正交对称矩阵，即
变号次数 行列变号次数乱序

根据第二条性质和3.5.3节中的公式，二维哈达玛变换及其反变换可以写为

3.6.2 沃尔什变换

沃尔什变换是由哈达玛变换矩阵经过矩阵的初等变换（行变换）得到的。具体而言，就是将哈达玛变换的行重新排列，使得行的变号次数依次递增。

例如时

变号次数依次为0,1,2,3。

沃尔什变换也具有3条性质

性质 描述
递推性 可由哈达玛核间接递推得到
正交性 哈达玛变换矩阵为实正交对称矩阵，即
变号次数 行列变号次数依次递增

同样根据正交性和3.5.3节中的公式，二维沃尔什变换及其反变换可以写为

图像越平坦，经过沃尔什-哈达玛变换之后能量就越集中

3.7 KL变换

KL变换是基于图像统计特性的变换。KL变换能充分去除相关性，把有用的信息集中到数目尽可能少的主分量当中。

3.7.1 图像的统计参数

将一个的图像集合中每一个样本用一个列向量表示:

图像的协方差

其中，为集合的均值向量（对每个的行做平均，放入一个向量中），。

在有帧图像样本组成的集合中，可用如下两式近似求得和

因为协方差矩阵一定是实对称方阵（见随机信号处理第一章笔记），因此有个特征向量和对应的个特征向量。

3.7.2 离散KL变换

KL变换可以分为如下四步

第一步：计算图像集合的均值向量和协方差矩阵

第二步：计算的特征值并将其降序排序，计算特征向量并归一化特征向量

第三步：计算变换矩阵 对的特征向量进行归一化，将其按行拼接起来得到KL的变换矩阵。其中的归一化过程为

为阶的正交矩阵，因为特征向量之间是相互正交的，且有

第四步：计算KL变换

有了变换矩阵之后，KL变换表达式为

变换后图像的自协方差矩阵相当于对原图像的自协方差矩阵做对角化，求时，直接求的特征值即可

由此可见，KL变换对每个图像都要重新计算变换矩阵，因此KL变换不具备普适性。

3.7.3 KL变换的性质

性质1：因为是正交矩阵，所以离散KL变换时正交变换

性质2：由于二维KL变换核时不可分离的，所以KL变换是不可分离变换

4.7.4 主成分分析(Principal Components Analysis, PCA)

由于变换矩阵大小，与图像长宽呈平方关系，因此当图像较大时，计算复杂度呈上升。

PCA的核心思想是，图像能量主要集中在特征值较大的系数中，因此只用前个分量来近似表示图像，丢掉特征值较小的系数，对图像质量不会有太大影响。取前个特征向量对应的新的变换矩阵为

则新的变换为

这个式子的意义为用维向量代替原来的维的向量，称为主分量表示。

  1. https://zhuanlan.zhihu.com/p/141681355↩︎